9. Visualization: Seaborn

9.1. Quantities:

This type of graph shows the levels of variables. Also, these graphs show the variables according to categories or classifications.

import numpy as np
import pandas as pd
from pandas import Series, DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
import datetime as dt

The following database includes enaho modules (200, 300 and 500) for the period 2011 - 20119

enaho = pd.read_stata(r"../_data/enaho.dta")
enaho

	year	conglome	vivienda	hogar	ubigeo	codperso	dominio	estrato	panel	p203	...	acumulado	estud	educa	d_edu	exper	exper_2	tenure_2	edad_2	jefe	ubigeo_2
0	2011	0061	077	11	010701	04	selva	de 4,001 a 10,000 viviendas	2.011006e+14	hijo/hija	...	6.0	5.0	11.0	Secundaria completa	2.0	4.0	NaN	361.0	familiar	010000
1	2011	0110	112	11	010705	05	selva	Área de empadronamiento rural - aer compuesto	2.011011e+14	hijo/hija	...	6.0	5.0	11.0	Secundaria completa	3.0	9.0	9.0	400.0	familiar	010000
2	2011	0090	076	11	010205	03	selva	Área de empadronamiento rural - aer compuesto	2.011009e+14	nieto	...	6.0	5.0	11.0	Secundaria completa	5.0	25.0	36.0	484.0	familiar	010000
3	2011	0118	080	11	010401	03	selva	Área de empadronamiento rural - aer simple	2.011012e+14	hijo/hija	...	6.0	5.0	11.0	Secundaria completa	6.0	36.0	NaN	529.0	familiar	010000
4	2011	3408	066	11	010402	03	selva	Área de empadronamiento rural - aer compuesto	2.011341e+14	hijo/hija	...	6.0	5.0	11.0	Secundaria completa	3.0	9.0	0.0	400.0	familiar	010000
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
160767	2019	009703	084	11	250302	05	selva	401 a 4,000 viviendas	2.019010e+16	yerno/nuera	...	11.0	4.0	15.0	Universitaria incompleta	0.0	0.0	NaN	441.0	familiar	250000
160768	2019	009675	124	11	250107	03	selva	de 20,001 a 100,000 viviendas	2.019010e+16	hijo/hija	...	6.0	5.0	11.0	Secundaria completa	5.0	25.0	0.0	484.0	familiar	250000
160769	2019	009703	084	11	250302	04	selva	401 a 4,000 viviendas	2.019010e+16	hijo/hija	...	6.0	5.0	11.0	Secundaria completa	9.0	81.0	0.0	676.0	familiar	250000
160770	2019	009700	143	11	250301	03	selva	401 a 4,000 viviendas	2.019010e+16	hijo/hija	...	6.0	5.0	11.0	Secundaria completa	3.0	9.0	NaN	400.0	familiar	250000
160771	2019	009645	010	11	250101	02	selva	de 20,001 a 100,000 viviendas	2.018010e+16	hijo/hija	...	6.0	5.0	11.0	Secundaria completa	9.0	81.0	0.0	676.0	familiar	250000

160772 rows × 105 columns

Number of companies classification by number of workers hired

Microbusinesses < 10 workers ; Small businesses (10-20 workers); Medium businesses (21-100 workers); Big Businesses (>100 workers)

Why do many examples use fig, ax = plt.subplots() in Matplotlib/pyplot/python ?

https://stackoverflow.com/questions/34162443/why-do-many-examples-use-fig-ax-plt-subplots-in-matplotlib-pyplot-python

sns.set( style="darkgrid" )

#figure size

fig, ax = plt.subplots( figsize=(7,4) )

x = sns.countplot( x="empresa", data=enaho[enaho['year'] == "2019" ] )

plt.title('Cantidad de empresas según clasificación en el 2019')
plt.xlabel(' ')
plt.ylabel(' ')

Text(0, 0.5, ' ')

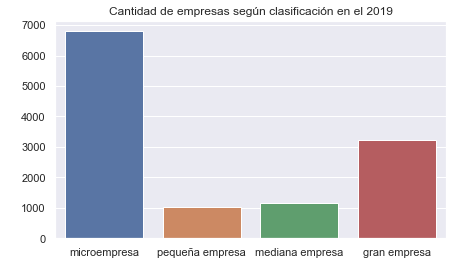
Vertical Countplot and one color (red)

sns.set(style="darkgrid")
fig, ax = plt.subplots(figsize=(7,4))

x = sns.countplot(y = "empresa", data=enaho[enaho['year'] == "2019" ], color = 'red')

plt.title('Cantidad de empresas según clasificación en el 2019')
plt.xlabel(' ')
plt.ylabel(' ')

Text(0, 0.5, ' ')

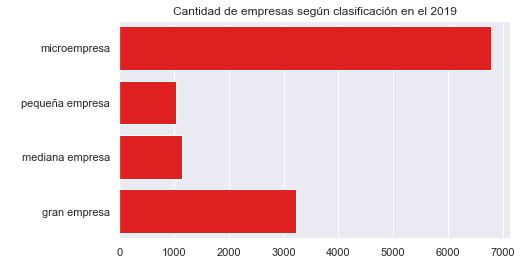
Evolutions of business in period 2017-2019

base2 = enaho[enaho['year'] > "2016" ]

fig, ax = plt.subplots(figsize=(10,6))

# hue: variable descomposition

ax = sns.countplot(x="empresa", hue="year", linewidth=1, data=base2)
plt.title('Evolución de las empresas en el périodo 2017-2019')
plt.xlabel(' ')
plt.ylabel(' ')
txt="Elboración propia - ENAHO (2011-2019)"  
plt.figtext(0.01, 0.01, txt, wrap=True, horizontalalignment='left', va="top", fontsize=10)

Text(0.01, 0.01, 'Elboración propia - ENAHO (2011-2019)')

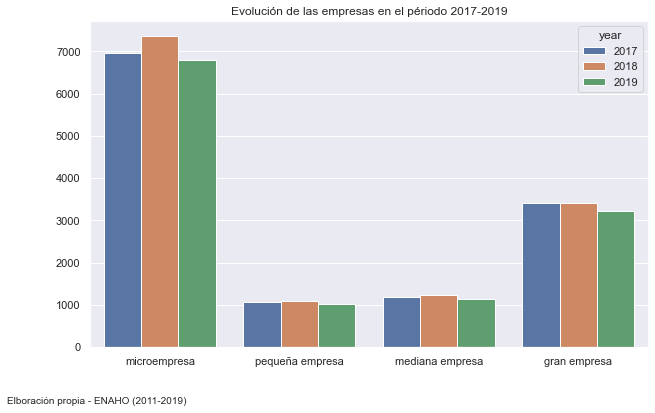
Number of companies by strata (urbano o rural) and evolution by years

hue = split in groups but in the same graph
col = create two new groups base in id group

ag = sns.catplot(x="empresa", hue="year", col= "area" , data= base2, kind="count", height=10, aspect=1);

(ag.set_axis_labels("", "Número de empresas")
  .set(ylim=(0, 6000))
  .despine(left=True)) 

<seaborn.axisgrid.FacetGrid at 0x2cbdeb45cd0>

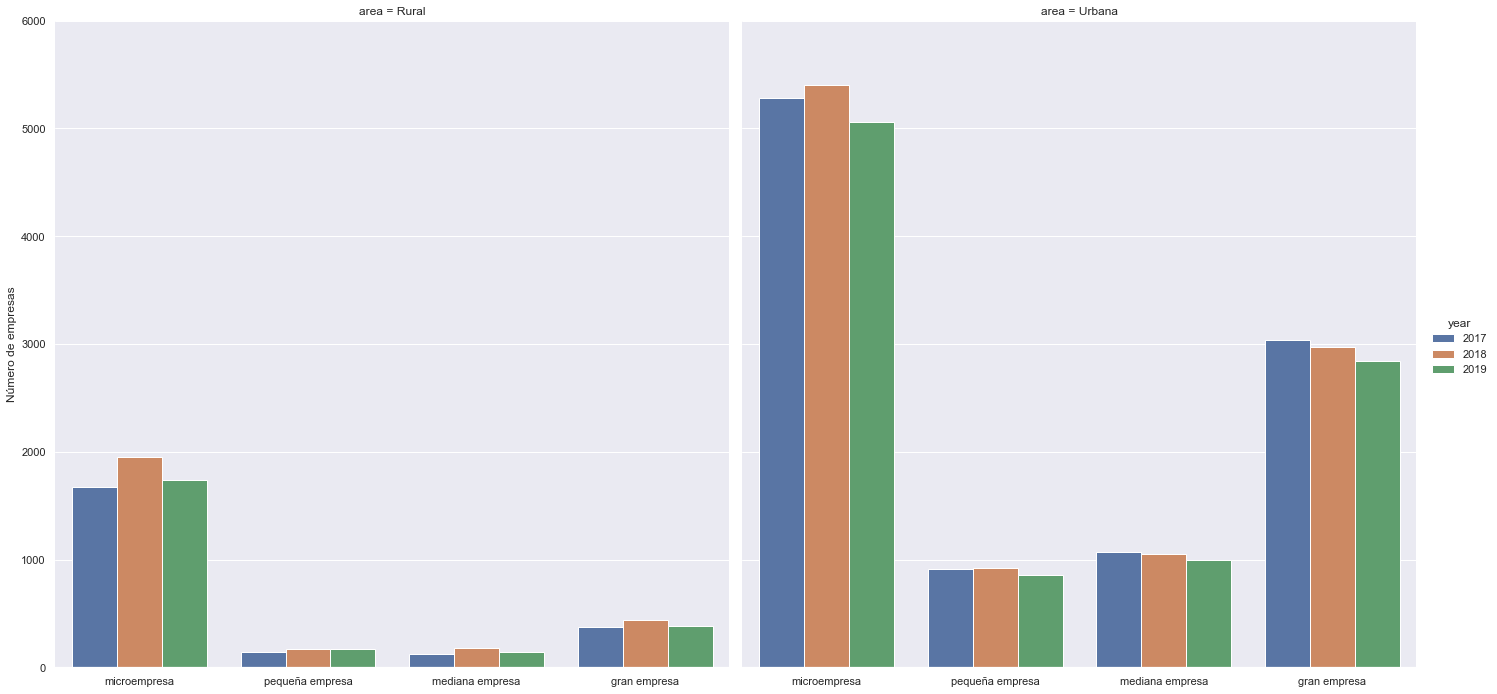
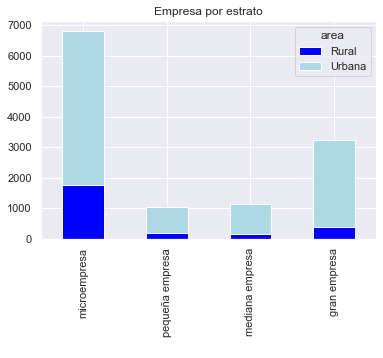
Number of businesses by strata - stacked bar plot

enaho['conglome']

0           0061
1           0110
2           0090
3           0118
4           3408
           ...  
160767    009703
160768    009675
160769    009703
160770    009700
160771    009645
Name: conglome, Length: 160772, dtype: object

enaho[ enaho['year'] == "2019" ].groupby( [ 'empresa', 'area' ] ).size().reset_index(name='num_firms')

	empresa	area	num_firms
0	microempresa	Rural	1742
1	microempresa	Urbana	5056
2	pequeña empresa	Rural	169
3	pequeña empresa	Urbana	857
4	mediana empresa	Rural	145
5	mediana empresa	Urbana	1000
6	gran empresa	Rural	381
7	gran empresa	Urbana	2846

# count businesses by strata using groubpy (similar collapse - stata)
#base_2 = enaho[ enaho['year'] == "2019" ].groupby( [ 'empresa', 'area' ], as_index = False )[['conglome'] ].count()
base_2 = enaho[ enaho['year'] == "2019" ].groupby( [ 'empresa', 'area' ] ).size().reset_index(name='num_firms')
base_2

	empresa	area	num_firms
0	microempresa	Rural	1742
1	microempresa	Urbana	5056
2	pequeña empresa	Rural	169
3	pequeña empresa	Urbana	857
4	mediana empresa	Rural	145
5	mediana empresa	Urbana	1000
6	gran empresa	Rural	381
7	gran empresa	Urbana	2846

# stacked information
base_3 = base_2.pivot(index = 'empresa', columns = 'area', values = 'num_firms')
base_3

area	Rural	Urbana
empresa
microempresa	1742	5056
pequeña empresa	169	857
mediana empresa	145	1000
gran empresa	381	2846

base_3.plot( kind='bar', stacked=True, title='Empresa por estrato', color = ['blue', 'lightblue'] )
plt.xlabel(' ')

Text(0.5, 0, ' ')

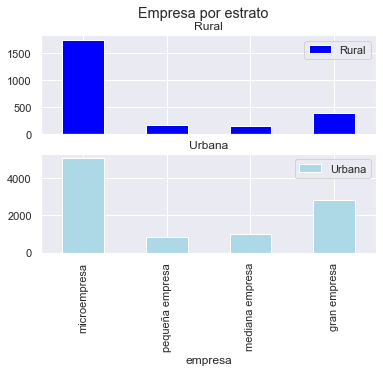
axes = base_3.plot( kind='bar', rot=0, subplots=True, color = ['blue', 'lightblue'], title='Empresa por estrato')
plt.xticks(rotation=90)

(array([0, 1, 2, 3]),
 [Text(0, 0, 'microempresa'),
  Text(1, 0, 'pequeña empresa'),
  Text(2, 0, 'mediana empresa'),
  Text(3, 0, 'gran empresa')])

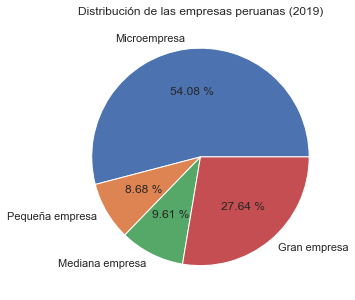
9.2. Proportions

Understandable plots to show categorical variables. Use this plots to explain participations from categories.

Pie

First at all, collapse dataframe to count categories of a variable

base = enaho.groupby([ 'empresa' ]).count()
base

	year	conglome	vivienda	hogar	ubigeo	codperso	dominio	estrato	panel	p203	...	acumulado	estud	educa	d_edu	exper	exper_2	tenure_2	edad_2	jefe	ubigeo_2
empresa
microempresa	58002	58002	58002	58002	58002	58002	58002	58002	58002	58002	...	57991	58002	57991	57991	57565	57565	58001	58002	58002	58002
pequeña empresa	9306	9306	9306	9306	9306	9306	9306	9306	9306	9306	...	9301	9306	9301	9301	9202	9202	9303	9306	9306	9306
mediana empresa	10304	10304	10304	10304	10304	10304	10304	10304	10304	10304	...	10302	10304	10302	10302	10212	10212	10304	10304	10304	10304
gran empresa	29642	29642	29642	29642	29642	29642	29642	29642	29642	29642	...	29639	29642	29639	29639	29392	29392	29640	29642	29642	29642

4 rows × 104 columns

# Labels to correct categories names 

labels=['Microempresa','Pequeña empresa' , 'Mediana empresa', 'Gran empresa']

plt.figure(figsize=(5,5))

ax = plt.pie(base['conglome'], labels=labels, autopct='%.2f %%')
plt.title('Distribución de las empresas peruanas (2019)')
plt.show()

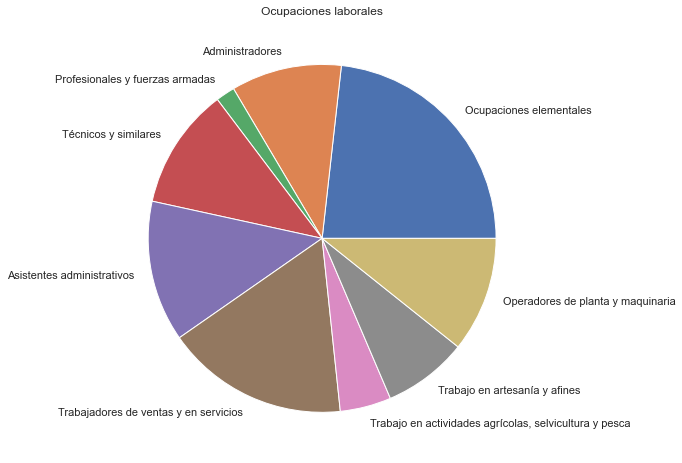
base = enaho.groupby('labor').size()

base.plot(kind='pie', subplots=True, figsize=(8, 8))
plt.title("Ocupaciones laborales")
plt.ylabel("")
plt.show()

Donuts

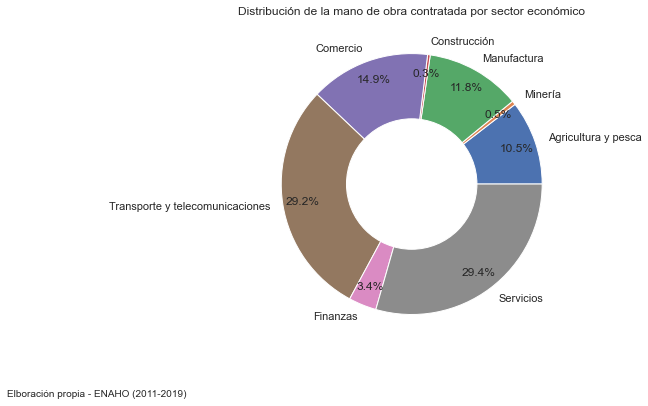
base2 = enaho.groupby([ 'sector' ]).count()

labels=['Agricultura y pesca','Minería','Manufactura','Construcción','Comercio','Transporte y telecomunicaciones', 'Finanzas', 'Servicios']
plt.figure(figsize=(10, 6))

ax = plt.pie(base2['conglome'], labels=labels,
        autopct='%1.1f%%', pctdistance=0.85)
  
# centroid size and color

center_circle = plt.Circle((0, 0), 0.50, fc='white')
fig = plt.gcf()

fig.gca().add_artist(center_circle)
  
plt.title('Distribución de la mano de obra contratada por sector económico')

# Adding notes

txt="Elboración propia - ENAHO (2011-2019)"  
plt.figtext(0.2, 0.01, txt, wrap=True, horizontalalignment='right', fontsize=10)

plt.show()

9.3. Distributions

Distribution plots visually assess the distribution of sample data by comparing the empirical distribution of the data with the theoretical values expected from a specified distribution.

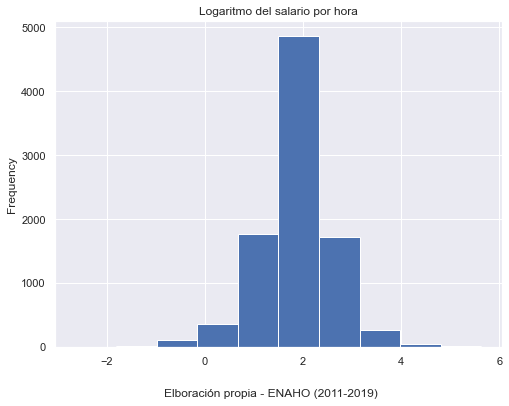
#filter database to 2019
base4 = enaho[enaho['year'] == "2019" ]


base4['l_salario'].plot(kind = 'hist', bins = 10, figsize = (8,6))
plt.title('Logaritmo del salario por hora')

txt="Elboración propia - ENAHO (2011-2019)"  
plt.figtext(0.5, 0.01, txt, wrap=True, horizontalalignment='center', fontsize=12)
plt.show()

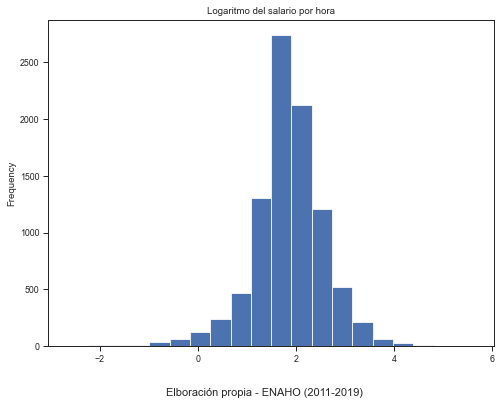
Reducing intervals

Frequency distribution with a smaller interval (lower relative frequency). Therefore, the height of each bar accounts smaller amount.

sns.set('paper')
sns.set_style("ticks")

base4['l_salario'].plot(kind = 'hist', bins = 20, figsize = (8,6))
plt.title('Logaritmo del salario por hora')

txt="Elboración propia - ENAHO (2011-2019)"  
plt.figtext(0.5, 0.01, txt, wrap=True, horizontalalignment='center', fontsize=11)
plt.show()

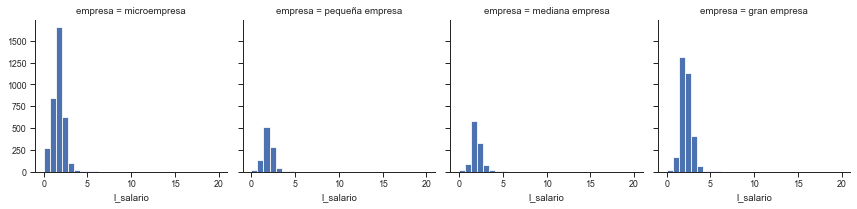
Multiple histograms

figure1 = sns.FacetGrid(base4, col="empresa", margin_titles=True)
figure1.map(plt.hist, 'l_salario', bins=np.linspace(0, 20, 30));

C:\ProgramData\Anaconda3\lib\site-packages\seaborn\axisgrid.py:703: FutureWarning: iteritems is deprecated and will be removed in a future version. Use .items instead.
  plot_args = [v for k, v in plot_data.iteritems()]
C:\ProgramData\Anaconda3\lib\site-packages\seaborn\axisgrid.py:703: FutureWarning: iteritems is deprecated and will be removed in a future version. Use .items instead.
  plot_args = [v for k, v in plot_data.iteritems()]
C:\ProgramData\Anaconda3\lib\site-packages\seaborn\axisgrid.py:703: FutureWarning: iteritems is deprecated and will be removed in a future version. Use .items instead.
  plot_args = [v for k, v in plot_data.iteritems()]
C:\ProgramData\Anaconda3\lib\site-packages\seaborn\axisgrid.py:703: FutureWarning: iteritems is deprecated and will be removed in a future version. Use .items instead.
  plot_args = [v for k, v in plot_data.iteritems()]

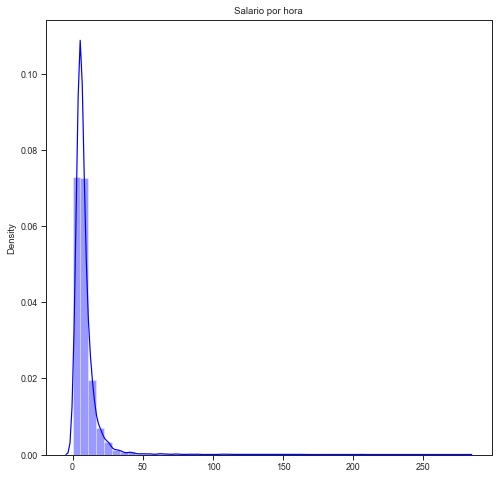
Real salary per hour density:

the distribution does not resemble a standard normal. The information is concentrated in lower values and there are some observations of high values.

plt.figure(figsize=(8, 8))

sns.distplot(base4['salario'], label = "Densidad", color = 'blue')
plt.title('Salario por hora')
plt.xlabel(' ')
plt.show()

C:\ProgramData\Anaconda3\lib\site-packages\seaborn\distributions.py:2619: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

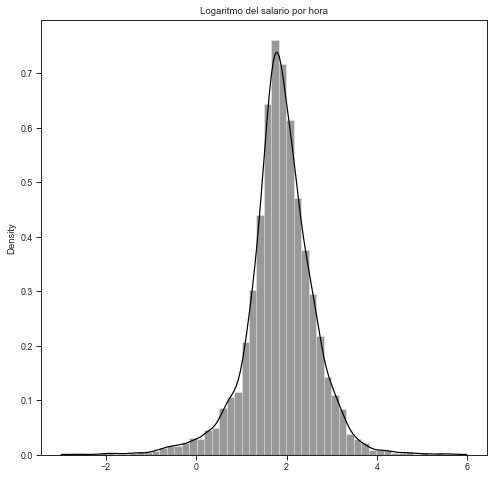
Logarithm of real hourly wage

This allows correcting the asymmetry presented by the original data.

#Alternative figure size
plt.figure(figsize=(8, 8))

sns.distplot(base4['l_salario'], label = "Densidad", color = 'black')
plt.title('Logaritmo del salario por hora')
plt.xlabel(' ')
plt.show()

C:\ProgramData\Anaconda3\lib\site-packages\seaborn\distributions.py:2619: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

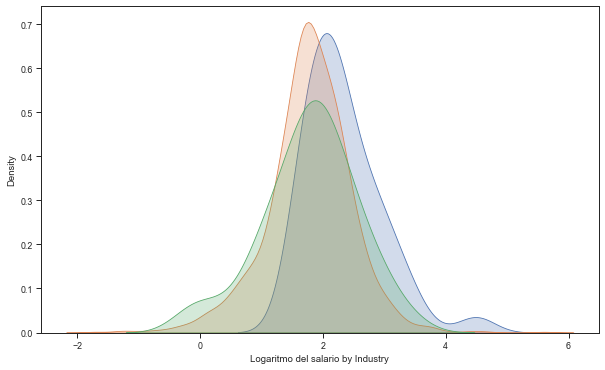
Real salaries for tres sectors (Construction, Mining and services)

plt.figure(figsize=(10, 6))

#Adding densities 

sns.kdeplot(base4.l_salario[base4.sector=='Construcción'], label='Construcción', shade=True)
sns.kdeplot(base4.l_salario[base4.sector=='Comercio, hoteles y restaurantes'], label='Comercio, hoteles y restaurantes ', shade=True)
sns.kdeplot(base4.l_salario[base4.sector=='minería'], label='Minería ', shade=True)
plt.xlabel('Logaritmo del salario by Industry')

# Construction sector shows certain stochastic dominance over mining and services

Text(0.5, 0, 'Logaritmo del salario by Industry')

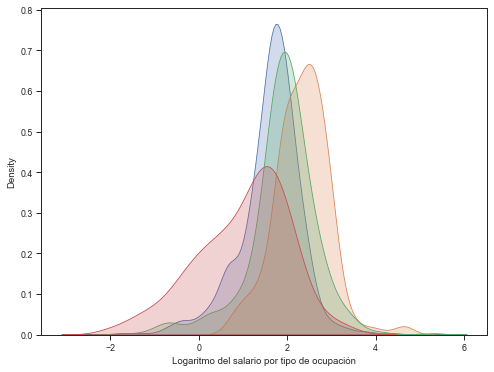
Labor occupations and real salary per hour densities

A For loop is used to include in the same graph the density function of hourly wages for different occupations.

fig, ax = plt.subplots(figsize=(8,6))
sector = [ 'Ocupaciones elementales', 'Profesionales y fuerzas armadas', 'Operadores de planta y maquinaria',
          'Trabajo en actividades agrícolas, selvicultura y pesca']
nombre = [ 'Ocupaciones elementales', 'Profesionales', 'Planta y maquinaria','Actividades extractivas']
    
for a, b in zip(sector, nombre):
        sns.kdeplot(base4.l_salario[base4.labor==a], label=b, shade=True)

plt.xlabel('Logaritmo del salario por tipo de ocupación')

# Two relevant findings: stochastic dominance of the salary of professionals and 
# concentration in lower levels of salary in the non-active primary sector.

Text(0.5, 0, 'Logaritmo del salario por tipo de ocupación')

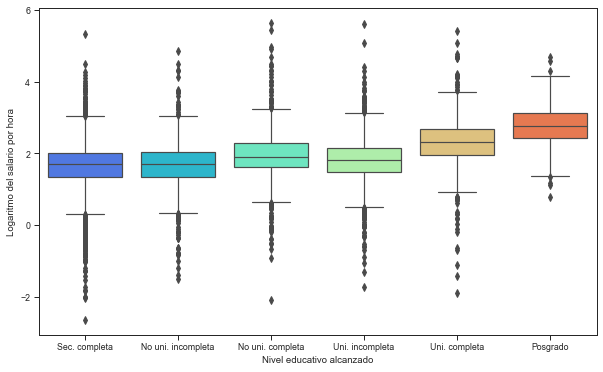
Box plot real salary and education

fig, ax = plt.subplots(figsize=(10,6))

box = sns.boxplot(x="educ", y="l_salario", data=enaho[enaho['year'] == "2019" ] ,palette='rainbow')
plt.xlabel('Nivel educativo alcanzado')
plt.ylabel('Logaritmo del salario por hora')
(box.set_xticklabels(["Sec. completa", "No uni. incompleta", "No uni. completa", "Uni. incompleta", "Uni. completa", "Posgrado"]))\

# The real wage quartiles are increasing with the educational level.
# Lower salary dispersion for the postgraduate level.

[Text(0, 0, 'Sec. completa'),
 Text(1, 0, 'No uni. incompleta'),
 Text(2, 0, 'No uni. completa'),
 Text(3, 0, 'Uni. incompleta'),
 Text(4, 0, 'Uni. completa'),
 Text(5, 0, 'Posgrado')]

9.4. Relationships

Charts used for both time series and cross-sectional data. These graphs allow to establish certain evidence of correlation or relationships between variables.

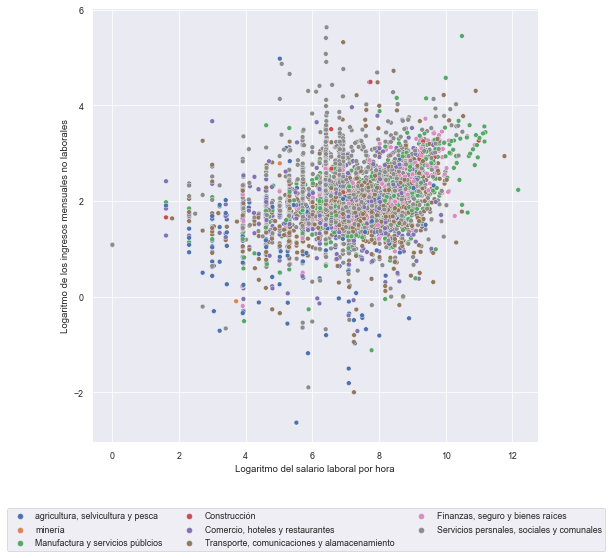
Scatter plot

First, a random sample is drawn from the original database. Subsequently, a dispersion graph is presented between the hourly wage (logarithm) and the non-labor monthly income (logarithm).

#Full sample

sns.set('paper')
plt.figure(figsize=(8, 8))
plot = sns.scatterplot(data=base4, x="l_n_labor", y="l_salario", hue="sector", palette="deep")

plt.xlabel('Logaritmo del salario laboral por hora')
plt.ylabel('Logaritmo de los ingresos mensuales no laborales')

# By default legend inside plot. Following codes allow us to put outside. 
# bbox_to_anchor: box location
# ncol: # columns of legend



plot.legend(loc='center left', bbox_to_anchor=(-0.2, -0.2), ncol=3);

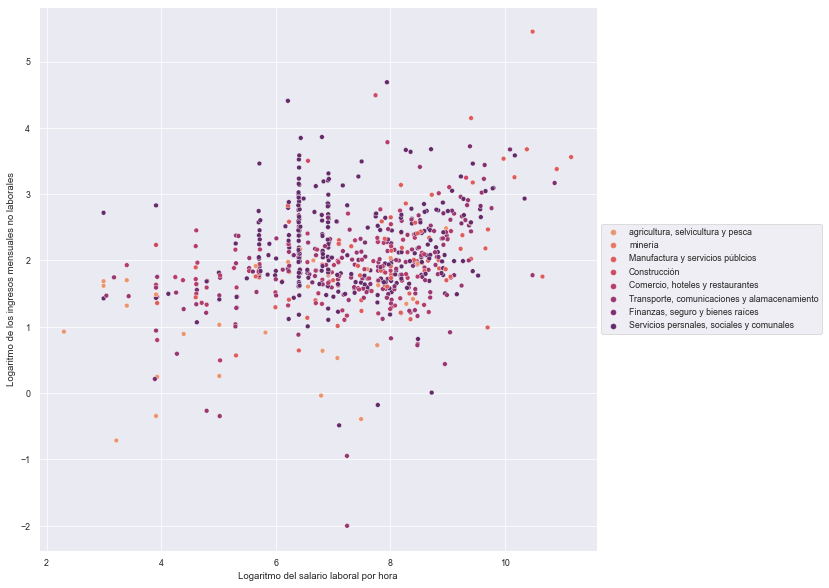
# Ramdon sample n = 3000

base5 = base4.sample(n = 3000)

sns.set('paper')
plt.figure(figsize=(10, 10))
plot = sns.scatterplot(data=base5, x="l_n_labor", y="l_salario", hue="sector", palette="flare")

plt.xlabel('Logaritmo del salario laboral por hora')
plt.ylabel('Logaritmo de los ingresos mensuales no laborales')

plot.legend(loc='center left', bbox_to_anchor=(1, 0.5), ncol=1);

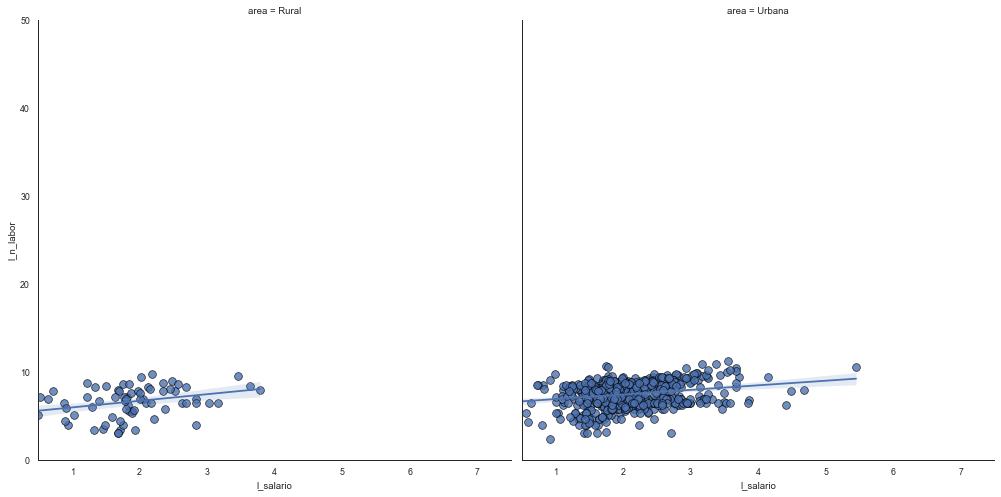
Reggresion real salary per hour and non-labor income by strata

s = The marker size in points**2.
linewidths = “The linewidth of the marker edges.”

sns.set_style("white")
gridobj = sns.lmplot(x="l_salario", y="l_n_labor", 
                     data=base5, 
                     height=7, 
                     robust=True, 
                     palette='Set1', 
                     col="area",
                     scatter_kws=dict(s=60, linewidths=0.7, edgecolors='black'))

gridobj.set(xlim=(0.5, 7.5), ylim=(0, 50))
plt.show()

Macroeconomics

• IMP: log-Commodity price index

• TC: log-exchange rate

• RIN: log-international reserves

• IPC: log-price consumption index

• RATE: central bank rate reference

• D: Annual difference

macro = pd.read_csv(r"../_data/macroeconomia.csv")
macro['YEAR']  = pd.to_datetime(macro['Fecha'])
macro

	Fecha	IPM	TC	RIN	IPC	RATE	DIPM	DTC	DRIN	DIPC	YEAR
0	2003-1	2.83506	1.25634	9.18519	4.41828	3.7500	13.73166	0.83108	12.50532	2.25690	2003-01-01
1	2003-2	2.85371	1.25004	9.21777	4.42295	3.8000	12.48664	0.16400	13.17984	2.76396	2003-02-01
2	2003-3	2.84717	1.24993	9.24303	4.43407	3.8200	7.76170	0.65330	17.18115	3.33857	2003-03-01
3	2003-4	2.80982	1.24554	9.24188	4.43356	3.8400	1.97256	0.69980	13.92729	2.56103	2003-04-01
4	2003-5	2.88617	1.24686	9.23065	4.43324	3.7800	6.81493	0.92160	12.37214	2.39028	2003-05-01
...	...	...	...	...	...	...	...	...	...	...	...
199	2019-8	3.74485	1.22252	11.12236	4.88368	2.5642	3.71183	2.73013	12.37958	2.01920	2019-08-01
200	2019-9	3.74443	1.20844	11.12124	4.88375	2.5038	7.63091	1.29986	15.82517	1.83408	2019-09-01
201	2019-10	3.70510	1.20622	11.13029	4.88486	2.5045	0.48716	0.71850	15.12033	1.86310	2019-10-01
202	2019-11	3.69955	1.20500	11.11988	4.88594	2.2984	0.97267	-0.08858	11.80591	1.84959	2019-11-01
203	2019-12	3.73001	1.20204	11.13212	4.88809	2.2501	2.87310	-0.25863	12.80208	1.88227	2019-12-01

204 rows × 11 columns

sns.set('notebook')

sns.relplot(x="YEAR", y="IPM", kind="line", color="red", data=macro, height=5, aspect=2)
plt.xlabel(' ')
plt.ylabel(' ')
plt.title('Índice del precio de materias primas 2013-2019')

txt="Elboración propia - BCRP"  
plt.figtext(0.5, 0.01, txt, wrap=True, horizontalalignment='center', fontsize=12);

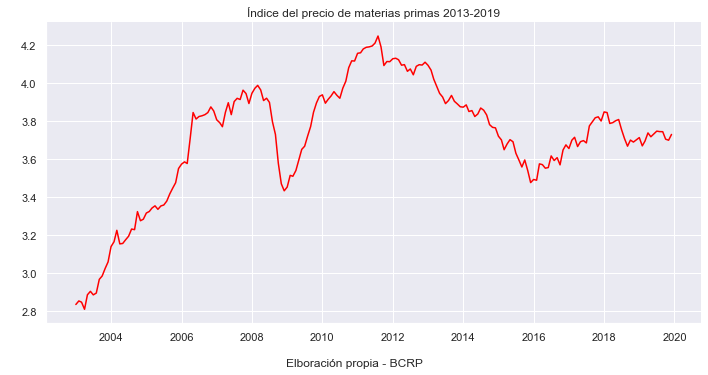
Series in a single image

This graph shows a positive relationship between the change in international reserves and the commodity index.

sns.set('notebook')


fig, ax = plt.subplots(figsize=(12,5))

x = macro['YEAR']
y1 = macro['DIPM']
y2 = macro['DRIN']

plt.plot(x, y1, label ='Indice de materias primas (Var %)', color='blue')
plt.plot(x, y2, label ='Reservas internacionales (Var %)', color='red')
plt.axhline(y=0, color='black', linestyle='--', lw=0.8)

plt.legend(loc='upper right')

txt="Elaboración propia - BCRP"  
plt.figtext(0.2, 0.01, txt, wrap=True, horizontalalignment='right', fontsize=10);

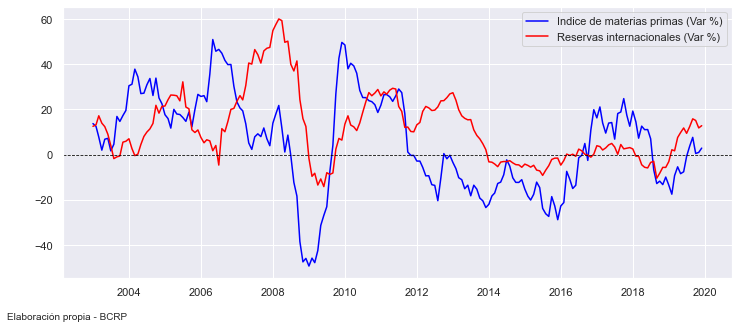
Dual-line Plots

Exchange rate and monetary policy reaction

sns.set('notebook', style = "ticks", font_scale= 1.08)

fig, ax = plt.subplots(figsize=(10,5))
lineplot = sns.lineplot(x= "YEAR" , y= "RATE", data=macro, 
                        label = 'Tasa interbancaria promedio ', color="k", legend=False)

#sns.despine()
plt.ylabel('Tasa de política monetaria')
plt.xlabel(' ')
plt.title('Exchange rate and monetary policy reaction');

ax2 = ax.twinx()
lineplot2 = sns.lineplot(x= "YEAR", y= "DTC", data=macro, ax=ax2, color = "red", 
                         label ='Tipo de cambio (variación anual %)', legend=False) 
sns.despine(right=False)
plt.ylabel('Tipo de cambio')
ax.figure.legend(loc='lower center', bbox_to_anchor=(1.1, 0.5), ncol=1);


txt="Elboración propia - BCRP"  
plt.figtext(0.2, 0.01, txt, wrap=True, horizontalalignment='right', fontsize=10);

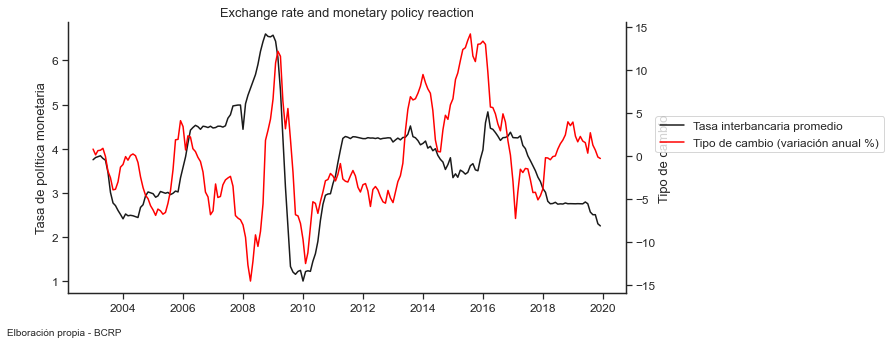
9.5 Reference:

Library of plots:

https://www.python-graph-gallery.com/stacked-and-percent-stacked-barplot

Seaborn package:

https://seaborn.pydata.org/generated/seaborn.catplot.html

https://programmerclick.com/article/54791895404/